[Coursera][Automata] 自動機理論-Automata筆記-第六週(上): Intractable Problems and NP-completeness

October 23rd, 2015

image

前言與心得整理

由於第六週的內容牽扯到P=NP相關理論還有NP-Complete的證明．所以我把內容拆成兩個禮拜，希望能夠更仔細地來了解這個部分．

相關文章

第六週前半部分的課程內容:

###Intractable Problems

P類問題

接下來會介紹一些需要耗費相當多的時間(指的是處理時間超過指數時間(polynomial-time)的問題．

回過頭來先要定義如何指出圖靈機的時間限制:

T(n): 指的是輸入w長度為n的時候，該圖靈機一定會停止的

這時候就會帶出第一個名詞: P 也就是如何定義一個問題是屬於P類的問題 (Class P problem)

	Class P:  指的是在DTM(Deterministic Turing Machine)下，其T(n)= polynomial-time (指數時間)

關於”P類”問題的範例

DTM可以被來當成是否可以用DFA(Deterministic Finite Automata_來表示其狀態的TM(Turing Machine)． 所以其實要尋找類似的範例其實不難，只是該問題必須要是在指數時間才能解決的，課堂上提供的範例如下:

  • 在CFG的 L(G) 給予一個字串w．判斷w in L(G)
    • 之前有提過要快的話，必須使用CYK演算法．然後其時間複雜度為O(n^3)

NP類問題

在介紹NP類問題前，雖然課堂上老師直接透過背包問題(Knapsack Problem)來引導NP類問題．不過我個人認為，還是需要簡單的瞭解一下`NP類問題｀的定義:

	Class NP: 指在NTM(Nondeterministic Turing Machine)下，其T(n)為指數時間(polynomial-time)

沒有錯，P類問題與NP類問題最大的差異是TM讀入一個輸入的時候．其反應是唯一的(DFA)或是多重的(NFA)． 接下來就可以將背包問題(Knapsack Problem)開始帶入:

什麼是背包問題(Knapsack Problem)

關於背包問題的定義，種類與範例．其實這一篇台師大的文章講得非常好．這裡僅僅簡單的帶過:

背包問題: 將一堆東西放進背包，每一件物品有它的重量與價值，透過有限制重量的背包來取得放入價值的最大化．

解法與時間複雜度: 對於背包問題的解法，一般而言就是透過動態規劃(Dynamic Programming)的方式來找．如此一來: 如果有n個物件，就必須要找出該物件放進背包與不放進背包的價值．所以時間複雜度為O(n * 2^n) (2是因為要計算 出現與不出現．必須要反覆計算n回)

P = NP ?

接下來就帶入大家都了解的P=NP這個被稱為史上七大難解問題之一． 究竟P是不是相同於NP？ 其實課堂上也有一些簡單的討論．

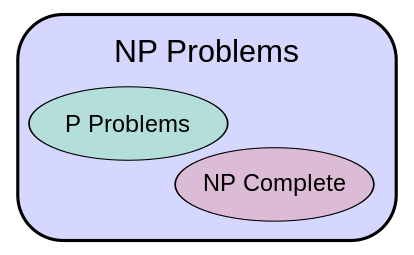
取自Wiki，NP-Complete 概念

以上的圖是來是Wiki，主要是講解如果認為P不等於NP的時候．他的概念是以這樣的方式作為出發來討論．

NP-Complete Problem

首先要討論P是否相同於NP，可以透過一個面向來探討．就是透過NP完全(NP-Complete Problem)．

A decision problem C is NP-complete if:

  • C is in NP, and
  • Every problem in NP is reducible to C in polynomial time

這是從NP-Completeness看到比較formal的定義．也就是說，如果我們能夠透過polytime reductions的方式來朝向證明NP-Completeness

Polytime Reductions

Polytime Reductions 又稱為Polynomial-time reduction，以下會解釋這種reduction 的目標與方法:

目標: 如果可以找到一個方式將所有的NP問題歸約(reduction)成語言L，並且能夠找到多項式的解決時間(Polytime)．那麼就可以找到多項式的演算法(deterministic polytime algorithm)來計算所有的NP問題．

簡單的來說:

  • 只要能夠找到一個方式來將所有的NP -> (Polytime Reduction) L
  • 只要能夠找到Polytime Algorithm for L
  • 那麼就能夠推導出其他Deterministic Polytime Algorithm給所有的NP

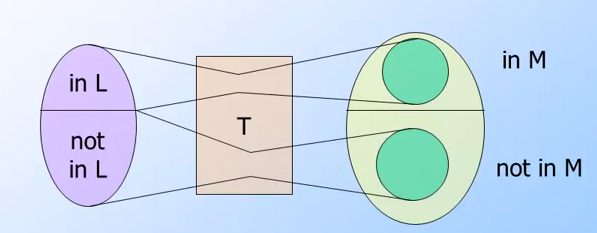方法:

  • 先定義有L與M兩種語言
  • L->(polytime reduction) M
  • Transducer
    • 先做Transducer將原本的資料由長度為n作轉換為x
    • 透過Transducer轉換的資料長度會大於n，但是會 <= p(n)
    • 將這系列動作既做 T(w) = x
  • 如果w是在L裡面，那麼透過這樣轉換出來的x 必定也在M裡面．

Proof that Polytime Reduction “Work”!!

要如何證明Polytime Reduction是有作用的．

  • 先定義有L與M兩種語言，其中:
    • L有輸入w其長度為n，M有輸入x
    • L有演算法p(n)， M有演算法q(x)
  • L->(polytime reduction) M
  • 可以透過transducer轉換出 p(n)=x
  • 可以計算出M的演算法為q(x) = q(p(n))
  • 全部的時間相同 L的計算時間+M的計算時間 = p(n) + q(p(n))
  • 已經知道 p(n)為polytime 並且也知道 q(p(n))也為polytime
  • p(n) + q(p(n)) 也是 polynomial time

The Satisfiability Problem (SAT)

SAT是NP問題裡面的最常被提到的問題之一，而所謂的SAT就是給予一個運算式來(ex: (x+y)(-x + -y) ) 來尋找該式子為true的狀況，該x與y的組合． 這個範例裡面，解答為:

  • x=0; y=1
  • x=1; y=0

注意: SAT裡面的優先順序是 NOT(!)->AND(.)->OR(+)

講解Cook-Levin理論 (或稱為Cook’s Theorem)

講解Cook-Levin理論提供了一個方式來證明SAT是NP-Complete(NP完全問題)．

個人很推薦這段兩分鐘的Youtube: Cook’s Theorem，裡面雖然沒有講解Cook’s Theorem的流程，但是把主要精神講解出來．（重點是他只有兩分鐘)

Cook’s Theroem 準則

，Cook–Levin理論提供了很不同的思路去解決SAT是NP-Complete的問題(不過人家也花了十一年)．也就是透過演算法轉換的方式來證明這個問題是NP-Complete，而不是直接去證明這個問題是NP-Complete（from wiki)

  • 已知一個NP-Complete的問題必定存在一個Algorithm，可以在Polytime解決這個NP-Complete問題．
  • 如果能夠把任何演算法透過圖靈機轉換成 Boolean Formula(一個布林方程式是否存在解)
  • 那麼也就能證明這個問題是NP-Complete

NTM(Nondetermistic Turing Machine) for SAT

透過這樣的思路，完整定理是:

	讓L屬於NP，而M代表NTM(Nondeterministic Turing Machine)．我們需要設計一個L，並且使得它的time-bond <= p(n) (其中n是輸入的個數)，並且 p 是 polynomial．

關於詳細的證明流程，我還在仔細研究．目前看了好幾份slide跟課程都無法正常理解． 證明 NP-Complete 陷入了一個 各家slide 方向與準則相同… 但是沒有一家證明流程是一樣的 XDD

希望下周可以完成．

程式作業/Homework

下週再做Homework

相關程式

本週相關程式，是把NP問題中的PCP拿來當作練習的題目． 本來很好奇為何在網路上沒有找到比較好的解法． 仔細研究才發現PCP(Post’s Correspondence Problems)其實還沒有一個比較好的解法． 主要原因可能因為PCP本身有太多比較難以解決得部分，比如說:

  • 判定錯誤的停止條件． 由於PCP是NP問題，而且又是屬於Recursively enumerable language (根據我了解的定義） 所以它無法正確的知道，何時可以停止(halt)
  • 目前判斷了循環的一個case，根據我這星期研究PCP循環的case可能目前只發現兩個 (1) 解答循環 (2) 一方的長度無限制延長..

我的解法在這裡，https://github.com/kkdai/pcp 不是一個完整解法，但是持續研究如何解決．

參考網址

Buy Me A Coffee

Evan

Attitude is everything