[Coursera][Automata] 自動機理論-Automata筆記-第四週: Pushdown Automata and Properties of Context-Free Languages

October 10th, 2015

image

前言與心得整理

進入到第四週，這個章節會透過深入了解PDA(Pushdown Automata)來導入CYK演算法與計算機的基礎- 圖靈機(Turing Machine)． 算是我一開始就相當期待的課程．

相關文章

第四週課程內容:

Equivalence of PDA’s and CFG’s

主要這個章節是會提到如何將CFG(Context-Free Grammar)轉換成 PDA(Pushdown Automata)， 首先先來符號介紹:

  • L(G): 屬於CFG G所以符合的Language L
  • 我們想要透過 PDA P來找出一個轉換方式可以產生 N(P) = L
    • 在這個 PDA(P)裡面有:
    • start node q
    • 所有的輸入symbol 屬於 G
    • 相同的stack會存入的就是symbol所以也是從G挑出來
    • 一開始的symbol也是從G挑出來．

範例:

  • CFG: S->Aa ; A->cc
  • Stack start symbol: S
  • Input: acc

以下分開成δ()與stack狀態

  • δ(q, a, S), stack: [S], input: cc (輸入a 進去了)
    • 這時候會從input 移除a, S 可以轉換成 Aa
    • 去除掉a stack剩下 [A]
  • δ(q, c, A), stack: [A], input: c
    • 這時候轉換A->cc
    • 並且一個c 被input 修除
  • δ(q, c, c), stack: [c], input: ε
  • δ(q, ε, ε), stack: [ε], input: ε

於是結果為Stack變更的流程為: [S]->[aA]->[A]->[cc]->[c]->ε

Convert PDA to CFG

接下來要來將PDA的轉換式，轉換成CFG．根據定義我們會從

    L = N(P)

來建立相同L的 CFG G，並且滿足 L(G) = L = N(P)．

首先這裡有一個假設 [pXq] 指的是從pstate透過輸入X可以到q state．

範例:

    δ(p, a, X) contains (q, ε) 可以表示  [pXq]->a
  • 就是所有從p輸入a的時候
  • 此時stack裡面有X． 而且可以到達q
  • 使得stack 為空 (ε)．就可以求得 [pXq]->a

範例

    δ(p, a, X) contains (r, Y) 可以表示  [pXq]->a[rYq]
  • 是p透過a會先到達r(此時會先把X從stack pop出來)
  • 而且stack 剩下Y(表示有push Y)
  • 所以是production 是 [pXq]->a[rYq]
  • 也就是說如果要達到q還必須要輸入Y才能夠從r到達q．

The pumping lemma for CFL’s

首先先來回顧一下，什麼是pumping lemma:

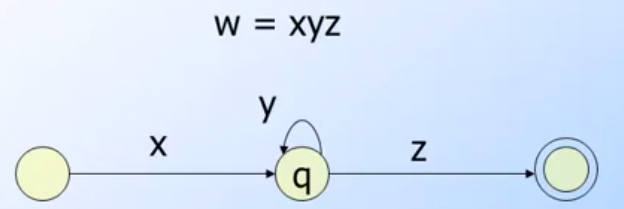
image

  • 在一個Regular Language其中有著n個狀態，在字串長度w > 輸入個數的時候，總能夠找到 xyz 符合:
  • w = xyz
  • xz <= n
  • y > 0
  • For all i>=0 xy^i z is in L

同樣的在CFG(Context-Free Language)一樣也能夠找到Pumping Lemma只是有不同的是:

    同樣的RE Pumping Lemma定義下 y 有兩段 z=uvwxy
  • 在一段CFL之中，有著n個數字．如果字串z>=n則存在z=uvwxy 其中
  • vwx <= n
  • vx >=0
  • For all i >=0; uv^i wx^i y in L

Decision and closure properties for CFL’s

如何證明字串w是不是屬於L(G)，可以使用CYK algorithm． (它具有的時間複雜度為 O(n^3))

CYK Algorithm

CYK演算法可以來計算某些輸入字串是否符合CFG(Context-Free Grammar)．如同上勉提到的算法．如果最後計算出來的symbol沒有非終端的符號(non-terminal symbol，一般而言就是S)的話．就代表字串不能被CFG所產生．

一般而言，要計算某段文字是否能被CFG來產生，需要透過回朔法(backtracking)原本需要指數時間 O = C^n ．但是使用CYK可以把所需要得時間縮短到 O = n^3． 算是有相當程度的優化．

直接透過範例來解釋會比較容易了解:

範例:

    S->AB, A-> BC|a, B->AC|b, C-> a|b    input string w= ababa

解題流程

  • 首先先找 X_ii:
    • 拿出第一個input a，來找X_11:
      • 找出 A-> BC a 取出 A
      • 找出 C-> a b 取出 C
      • 於是 X_11 = {A, C}
    • 拿出第二個input b, 來找X_22:
      • 找出 B-> AC b 取出 B
      • 找出 C-> a b 取出 C
      • 於是 X_22 = {B, C}
    • 拿出第三個input a，跟第一個解法相同得到 X_33 = {A, C}
    • 拿出第四個input b，跟第一個解法相同得到 X_44 = {B, C}
    • 拿出第五個input a，跟第一個解法相同得到 X_33 = {A, C}
  • 接下來要找 X_ij
    • 舉例要找出 X_12，需要參考 X_11 跟 X_22
      • 第一個symbol 要找 A 在X_11中(第一個)，B在X_22中(第二個)．能夠找到 AB的就是 S-> AB 於是得到S
      • 第二個symbol 要找 A 在X_11中(第一個)，C在X_22中(第一個)．能夠找到 AC就是 B-> AC 於是得到 B
      • 答案就是 X_12 = { S, B }
    • 舉例 X_23，需要參考 X_22 = {B, C}與 X_33 = {A, C}
      • 第一個symbol 要找 B在X_22(第一個) 找 C在X_33(第二個)，能夠找到 A->BC 於是得到Ababa
      • 第二個symbol 要找 B在X_22(第一個) 找 A在X_33(第一個) 沒有找到能夠推導出 BA的，於是沒有．
      • 答案: X_23 = {A}
    • 再舉例一個 X_34，需要參考 X_33={ A, C} X_44={B, C}
      • 第一個symbol 找 A在X_33 (第一個)再找 C在X_44(第二個) 於是要找 AC 得到B
      • 第二個symbol 找 A在X_33 (第一個)再找 B在X_44(第一個) 於是要找AB 得到S
      • 答案: X_34 = { B, S}
  • 依此類推….
  • 如果要找 X_13 就得找 X_12跟 X_23 其他步驟同上
  • 依此類推找到 X_15 為 {A}
  • 由於X_15的結果不含{S}，而是只有A．所以我們知道 w=ababa不存在這個L(G)裡面

Turing Machine

一開始先講解資料與程式相關的部分．其實編碼就可以視為是一種automata的轉換方式． 接下來有一些名詞解釋:

  • Finite Set 有固定長度的集合，裡面找不到任何一對一的關係．只是資料的集合．
    • 範例:
      • {A, B, C} 是一個 Finite Set而他的基數(cardinality)為3 (也就是集合中的元素個數)
  • Infinite Set 代表一個集合有一對一的關係，不論是對於自己或是其他集合．
    • 範例:
      • {1, 2, 3, 4, ….} 其中 1<->2, 2<->4
  • Countable sets 其中有一對一的正整數關係(並不是代表全部數字都是正整數，而是代表可以用正整數找出他們的關係)
    • 範例:
      • {0, -1 1, -2 2, ….} 其中 -1跟1 為 -i 與 i 的關係（i為正整數)

Turing Machine Theory

目的: 透過Turing Machine Theory可以證明特定的Language是否含有algorithm

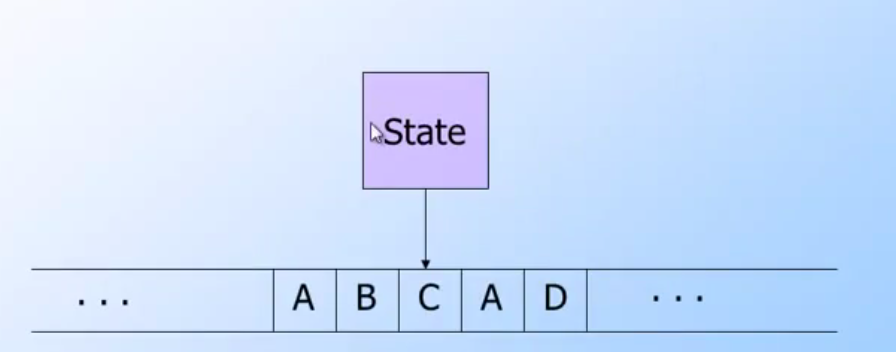
image

下面橫向的A,B,C,D 為 type是一個由已知的輸入符號({A,B,C,D})所構成的無止盡的集合．根據這張圖，Turing Machine Theory主要是根據輸入的symbol(下方的ABCD)與本身的狀態來改寫symbol(就是會改寫下方的輸入)並且檢查是否會到達final state．這樣的計算方式可以被用程式語言來實現，而且這樣的計算比較簡單與易懂．

基本原理很像PDA(Pushdown Automata)不過TM(Turing Machine)本身會改寫symbol．圖靈機(Turing Machine)被認為是電腦架構的原型，主要有以下幾個因素：

  • 輸入: 透過Type的輸入，可以將資料輸入到電腦．
  • 處理: 圖靈機會根據輸入來做相對地移動或是動作（改寫資料）
  • 狀態: 這也是圖靈機跟其他不同是，一般而言輸入1或是輸入0應該都要能夠期待有相同的結果．但是由於有狀態概念，所以相同輸入在圖靈機不一定會有相同的動作(除非狀態也相同)．

範例

  • 主要需求:
    • TM來判別一連串的輸入是否有1，如果遇到輸入為1就停止並且接受．
    • 全部輸入為 {0, 1, B(空白)}
  • 邏輯:
    • 如果遇到輸入為0，繼續向又去找
    • 如果遇到輸入為B，退回一部，並且將B改成1
    • 如果遇到輸入為1，停止並且接受．
  • 輸入:
    • 全部輸入為{BB00BB}，從第一個0開始．

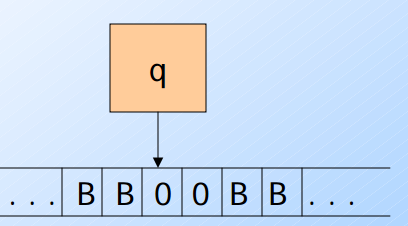
image

  • 透過轉換式(transition function)來表示:
    • δ(q, 0) = (q, 0, R) (其中R代表方向，向右) 此時輸入剩下 0BB
    • δ(q, 0) = (q, 0, R) (其中R代表方向，向右) 此時輸入剩下 BB
    • δ(q, B) = (q, B, L) (其中L代表方向，向左) 此時輸入剩下 01B
    • δ(q, 0) = (q, 0, R) (其中R代表方向，向右) 此時輸入剩下 1B
    • δ(q, 1) = (f, 0, R) (其中R代表方向，向右) 此時輸入剩下 B，因為到達f所以結束．
  • 透過ID( Instantaneous Descriptions)來表示目前狀態
    • 不同於PDA裡面的ID，這裡的ID是透過 q00 來代表 (目前狀態是q 即將輸入的symbol 為 00)
    • q00 (goes to) 0q0 (goes to) 00q(注意其實q右邊還有blank)(goes to) 0q01 (goes to) 00q1 (goes to) 000f

Formal Definition of Turing Machine Moves

  • δ(q, Z) = (p, Y, R)
    • 可以寫成 aqZb (goes to) aYpb
    • 如果Z等同於B(blank)也可以寫成 aq (goes to) aYp (b被消除)
  • δ(q, Z) = (p, Y, L)
    • 可以寫成 aqZb (goes to) apYb
    • 對於任何X aXqZb (goes to) apXYb

演算法(Algorithm)可以視為是一個TM(Turing Machine)，並且能夠到達的被接受與停止(f)的狀態．

L = L(M) 如果M為一個演算法，我們可以說L是一個Recursive Language． 所以我們可以說:

  • CFL(Context-Free Language)是一個recursive language．使用CYK演算法．

程式作業 (CYK演算法)

這星期的作業是講CYK演算法， 其實不算是太困難，不過題目裡面的資料呈現方式相當的詭異．竟然是用三個陣列來表示． S->AB 這樣的概念． 這樣在寫作上會比較困難，

作業本身就是要熟悉這樣的資料方式．與表現symbol的方式來做出CYK演算法．我將會在下一個章節的相關程式使用Go來完成CYK演算法．

主要概念與解法提示:

  • 記得要從 X_11 X_22 X_33… 先算
  • 再來算 X_12 X_23 X_34
  • 比較需要注意的是，由於資料表示用 [0]表示S [1]表示B．所以 S必定在B的前面，但是這個問題要解決，不然計算答案會錯．
  • 這邊要提醒，其實除了 X_11 X_22 以外，其他計算的時候都需要有展開多項式

’’’

k= j-i
X_i,j = (X_i,i+k-1,  X_i+k,j) | k=1  聯集  (X_i,i+k-1,  X_i+k,j) | k=2....	   '''
  • 更多部分可以參考 wiki

相關程式

本週的相關程式，主要是使用第一次的程式作業的內容， 第一次程式作業主要是將RE -> Epsilon-NFA． 作業雖然很簡單，但是作業本身就是一個值得學習的課題．

有興趣可以參考這裡https://github.com/kkdai/re2epsnfa

參考網址

Buy Me A Coffee

Evan

Attitude is everything