[Coursera][Automata] 自動機理論-Automata筆記-第一週Finite Automata

前言

主要是因為有大師推薦，然後發現這堂課的教授就是所謂的Compiler恐龍課本的作者Jeffrey Ullman(Compiler Design的聖經)． 加上自動機本身不僅僅實作牽扯到regular expression之外，更在分散式系統中的狀態機(state machine)扮有相當重要的部分． 所以需要來好好學習．

課程鏈結在這裡https://class.coursera.org/automata-004．

相關文章

• [Coursera][Automata] 自動機理論-Automata筆記-第一週Finite Automata(本篇)
• [Coursera][Automata] 自動機理論-Automata筆記-第二週: Regular Expression
• [Coursera][Automata] 自動機理論-Automata筆記-第三週: Context-Free Grammars and Pushdown Automata
• [Coursera][Automata] 自動機理論-Automata筆記-第四週: Pushdown Automata and Properties of Context-Free Languages
• [Coursera][Automata] 自動機理論-Automata筆記-第五週: Turing Machines and Undecidability
• [Coursera][Automata] 自動機理論-Automata筆記-第六週(上): Intractable Problems and NP-completeness
• [Coursera][Automata] 自動機理論-Automata筆記-第六週(下): Intractable Problems and NP-completeness

第一週課程

DFA(Deterministic Finite Automata)基本定義

• alphabet:
  • 任何有限的符號集合． (可以是ASCII也可以是Unicode)
  • ex: {0,1} (binary alphabet), {a,b} {s,p} 都是alphabet
• string:
  • 透過alphabet產生的list，其中每一個元素都要是該alphabet其中一個元素．
  • length代表的是該string有的個數．
    • ex alphabet {0, 1} 其 string {01} length=2
  • ε 代表是empty string其中他的length=0
• language:
  • 為alphabedt產生出所有string的subset．
• DFA: Deterministic Finite Automata: A formalism for defining languages．由以下組成:
  • 有限的狀態(states) 表示為 Q
  • 固定的input alphabet 表示為 Σ
  • 一個起始狀態 (start state) 表示為q0
  • 至少一個結束狀態 (final state) (這裏指的final state也是指可接受的狀態) 表示為 F
  • 一個transition function 表示為 δ(Q, A)其中 A 代表是一個輸入的 alphabet
    • transition function代表的是，一個輸入所要進入的一個狀態．
    • δ(Q, A) 代表是從狀態Q透過輸入A來計算下一個狀態會是哪裡．

範例:

{0, 1} 是一個alphabet

{0, 1}* = {ε, 0, 1, 00, 01, 10, 11, 010, …} 是alphabet {0,1}為可能出現的string組合，其中

• {e} length=0
• {0} length=1
• {00} {01} {10} {11} length=2

如果要討論language，我們可以說 {ε, 0, 1,00,01,10,11} 是我們將要用到的language

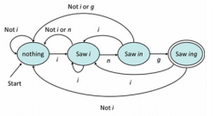
(pic: from coursera automata course lecture)

以上的圖，代表一個簡單的DFA，其中:

• 輸入alphabet為{0, 1}
• final state為 B
• dead state為 C (dead node: 也就是只走到C後不論怎麼輸入都無法到達final note)
• start state為 A
• transition function可以表示以下方式: A -> δ(B, 1) -> δ(C, 1)

根據以上的圖形，其實可以表示成另外一種表格方式(Transition Table):

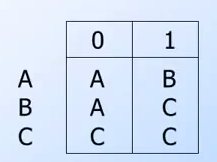
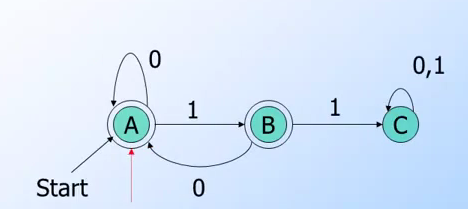
(pic: from coursera automata course lecture)

左邊為所在的狀態節點，右邊為透過輸入0或是1將要到的狀態節點．

Transition Table 簡單範例

• 在A狀態輸入0會回到A狀態，輸入1會到B狀態．
• 狀態A輸入1, 1 會到狀態C。

Transitio Function 運算範例:

• δ(B, 011) -> δ(δ(B, 01), 1) -> δ(δ(δ(B, 0), 1), 1) -> δ(δ(A, 1), 1) -> δ(B, 1) -> C
• δ(A, 0) -> A

NFA(Nondeterministic Finite Automata)基本定義

NFA跟DFA有些許的不同，這裡先列出幾個幾本定義

• NFA中，可以同時存在多個狀態中，也就是說δ(Q1, A)有可能出現不僅僅一個狀態Q2，而是δ(Q1, A)-> {Q2, Q3}．這代表這裡有路可以從Q1透過路線A可以到達Q2跟Q3．
• 跟DFA一樣，NFA一樣開始在一個start state
• 跟DFA一樣，NFA一樣結束在一個以上的final state

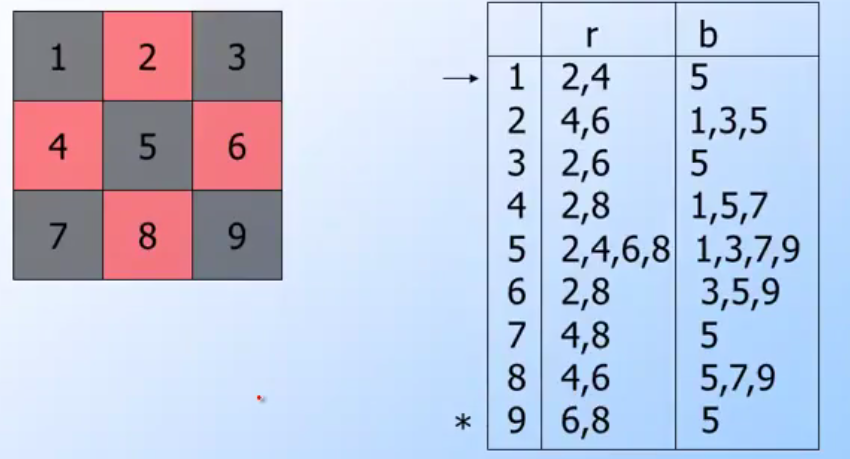
(pic: from coursera automata course lecture)

    NFA 表現起來，比較像是棋盤式．每一個狀態(格子)同一個輸入有不僅僅一個可以走得下一步(狀態)

如何把NFA轉化成DFA

從基本定義可以看得出來，NFA跟DFA的差異最大的就是:

• DFA: 每一次transition function會到唯一一個狀態，也就是: δ(Q1, A)-> Q2
• NFA: 每一個transition function不一定只會指向一個狀態，所以: δ(Q1, A)-> {Q2, Q3, ...}

也就是說，我們可以說任何一個DFA也可以說是一個NFA，也就是說只要DFA收到同樣的語言(language)由於輸入會是一連串，也就是說輸出也會是不僅僅一個狀態．也可以說DFA透過同一個language input可以轉換成NFA．

    δD(Q1, A) -> P
    δN(Q1, A) -> {P} 可以視為 P 為 所有輸出集合的其中一個

那麼要如何反過來將NFA轉換成DFA呢?

先就定義上的轉換

其實某種角度來說，如果把NFA的結果當成一個language的話，其實就可以被視為是DFA． 也就是說：

    δD(Q1, A) -> P     //一般習慣的DFA表示方式
    δN(Q1, A) -> {P}   //一般習慣的NFA表示方式

如果把{p}當成是一種state而非是一群state，這樣就可以把NFA表示式看成是另外一種DFA。 只是那麼transition function與transition table要如何運算呢? 這時候就需要用到subset construction．

Subset construction

δD({q1, q2, q3, ... qk}, A) 為一個將NFA轉換成DFA的transition function，而結果就是將所有結果的聯集合(union) i = 1, 2, 3 … k是 δN(qi, A)

也就是

    δD({q1, q2, q3, ... qk}, A) = union(δN(qi, A))  其中 i = 1, 2, 3 ... k

Subset construction的範例

透過以下的方式，我們可以將NFA的transition table，轉換成DFA的．

以下將每個流程，用文字敘述：

• 首先走到state {1} 這時候會透過 r 跟 b 走到 2,4 跟5 ． 由於我們要取每個結果的聯集．所以 {2,4} {5} 會被當作是我們的一個State．
• 接下來先走到 {2,4}, 這時候要查看 {2} 與 {4}的結果，也就是 將 {4,6}{2,8}做聯集{2,4,6,8}為r的結果，而將{1,3,5}跟{1,5,7}做聯集{1,3,5,7}．
• 並且將以上兩個結果當作新的state加入之後要走的路途
• 接下來走 {1,3,5,7} 於是又繼續看 {1} {3} {5} {7}的結果．以此類推….

會得到以下結果

ε-NFA 的基本定義

對於NFA，其實是可以允許不需要任何輸入的情況下狀態(state)自己改變． 這時候我們可以說是輸入為ε (因為 ε為空字串，代表的是沒有輸入)． 如此一來，所出現的NFA就稱為 ε-NFA．

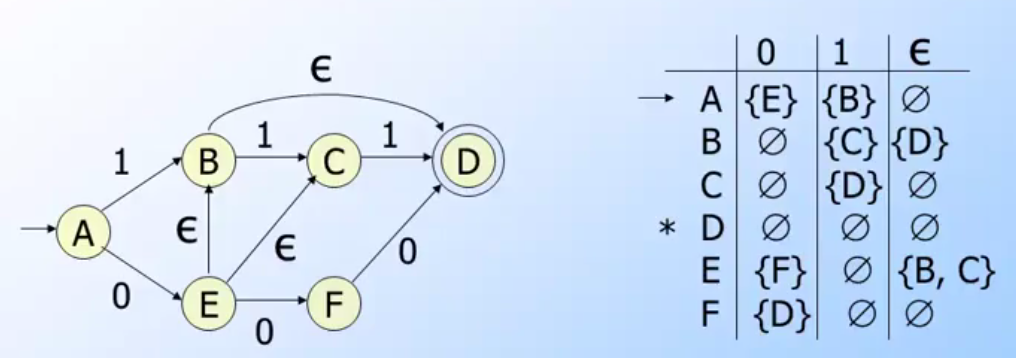(pic: from coursera automata course lecture)

最後我們會導出一個定義是

    每一個NFA都是ε-NFA

Closure of States : CL(q)

這裏同時會有一個新的函式 CL(q) : 其中CL(q)代表的就是 q 狀態的closure 也就是說透過q 所有不需要input能夠到達的state．（換句話說，也就是透過q 能夠透過輸入 ε 來到達的狀態． 也就是說 CL(q) = δN(q, ε)．

Example of Closure Starte

以上圖來說，這裡有一些Closure of States的範例:

• CL(A) = {A} 因為沒有任何ε 的輸入可以到達的狀態．
• CL(B) = {B, D} ，這裡δN(B, ε) -> D
• CL(E) = {B, C, D, E}

更多在ε-NFA關於transition function 的運算

• δ(q, w)在NFA中代表由狀態q開始透過輸入w，可以到達的狀態集合．
• δ(q, ε) = CL(q) 也就是說由狀態q 在沒有輸入(也就是說輸入為空集合ε)可以到達的狀態．
• δ(q, A) = δ(q, Aε) = δ(δ(q, A), ε) 所以可以推導出以下
• δ(q, A) = δ(δ(q, A), ε)) = CL(δ(q, A)) = CL({E}) (假設δ(q, A)={E})

關於第一週作業

這次作業主要都是一些基本觀念跟圖形來推到transition function 的結果． 主要是多看幾次就會找出來其中的規律性．（似乎也沒有方法論可以快速找到）．

相關程式

由於根據定義NFA與ε-NFA其實是無法去Implement的最後，我也把DFA的概念加以實現成一個小工具．放在https://github.com/kkdai/dfa

參考網址

• Coursera: Automata Course
• DFA: wiki