[Coursera][Automata] 自動機理論-Automata筆記-第二週: Regular Expression

前言與心得整理

進入到第二週，不知道會不會有更困難的主題出現．寫筆記寫著寫著，發現自己筆記內容比原本老師講的還要多，代表自己不懂得真的太多，需要不斷的補充資料來讓自己更清楚．

相關文章

• [Coursera][Automata] 自動機理論-Automata筆記-第一週Finite Automata
• [Coursera][Automata] 自動機理論-Automata筆記-第二週: Regular Expression
• [Coursera][Automata] 自動機理論-Automata筆記-第三週: Context-Free Grammars and Pushdown Automata
• [Coursera][Automata] 自動機理論-Automata筆記-第四週: Pushdown Automata and Properties of Context-Free Languages
• [Coursera][Automata] 自動機理論-Automata筆記-第五週: Turing Machines and Undecidability
• [Coursera][Automata] 自動機理論-Automata筆記-第六週(上): Intractable Problems and NP-completeness
• [Coursera][Automata] 自動機理論-Automata筆記-第六週(下): Intractable Problems and NP-completeness

第二週課程內容:

Regular Express 基本定義 與 運算

符號定義:

通常顯示E來表達一個regular expression，而L(E) 就表示一個regular expression 能表達出來的語言(language)．

Language的運算: (Union/Concatenation/Kleene Star)

• Union (U): 就是把兩個language做一個簡單的聯集．
  • ex: {01, 11, 101} U {10, 11, 101} = {01, 10, 11, 101}
• Concatenaion (LM): 把兩個language做一個連接，但是注意這裡跟字串的concatenation是不同的．基本定義而顏，把語言L跟語言M連接在一起就稱為LM． LM = wx | w in L and x in M．
  • ex:
    • L = { 01, 11}
    • M = { 10, 11}
    • LM = { 0110, 0111, 1110, 1111} 也就是 第一個L元素配上第一個M元素，第二個L元素配上第一個M元素．繼續類推．
• Kleene Star (*): 就是regex裡面的*，表達任何子集合在L中與空集合或是一個以上的子集合的聯集． L* = {ε} U L U LL ...
  • ex: L = {01, 11} L*= {} or {01, 11} or {0101, 0111, 1101, 1111} ....

Regular Expression定義

• a是一個symbol, 如果a是一個regular express(記作RE)，則 L(A) = {a}
• L{ε} = {ε}
• L(empty set) = empty set

將Langugage的運算套用過來，其中E1 跟 E2代表兩個RE:

• U運算： L(E1+ E2) = L(E1) U L(E2)
• Concatenation: L(E1E2) = L(E1)L(E2)
• Kleene Star (*) : L(E*) = (L(E))*

以下列出一些範例：

• 基本定義: L(0) = {0}, L(01) = {01}
• Union: L(01+0) = L(01) U L(0)= {01} U {0} = {01, 0}
• Concatenation: L(0(1+0))= L(0)L(1+0) = {0}{1,0} = {01, 00}
• Kleene Star: L(0*)={ε, 0, 00, 000, ... }
• 複雜一點的綜合運算： L((0+10)*(ε+1)) = L((0+10)*) L(ε+1) = L({0, 10}*) L(1)
  • 根據以上得結果，所有的Language，不論是0開頭或是1開頭，1結尾，但是只要沒有兩個連續的1就符合．
  • ex: {01} {0001} {0101010101}
  • 連續兩個1不再其中，因為是 ({0} + {10})* U {1}

將RE用ε-NFA表示:

要將RE(Regular Expression)用ε-NFA來表示，基礎的概念如下:

    邊線(arc)代表一個symbol，而路徑可以表示成 a, ε, empty set

(image from coursera Automata Course)

套用基礎運算的上如下:

Union: 就是一個分支的圖形

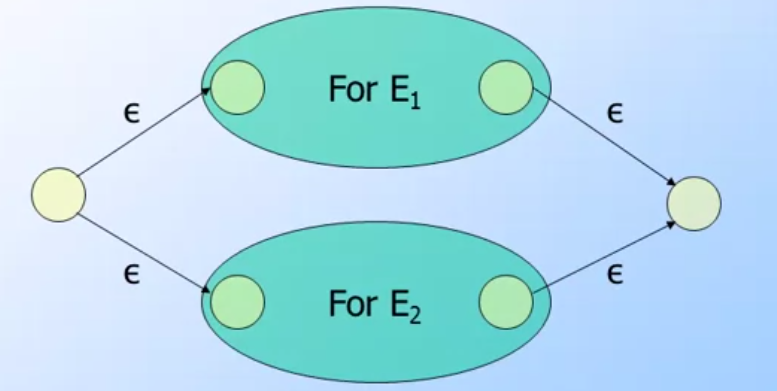
(image from coursera Automata Course)

Concatenation: 就是一個連接的圖形

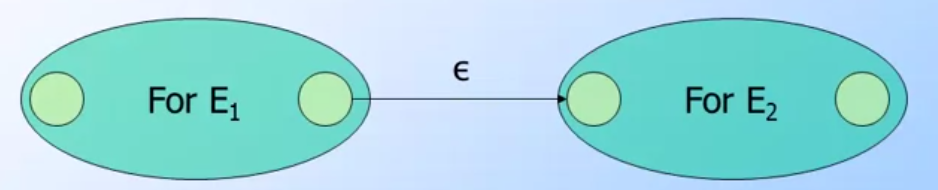
(image from coursera Automata Course)

Closure: (CL) 就是一個自己與自己迴圈的圖形(簡單來說 Kleene Star -> Closure)

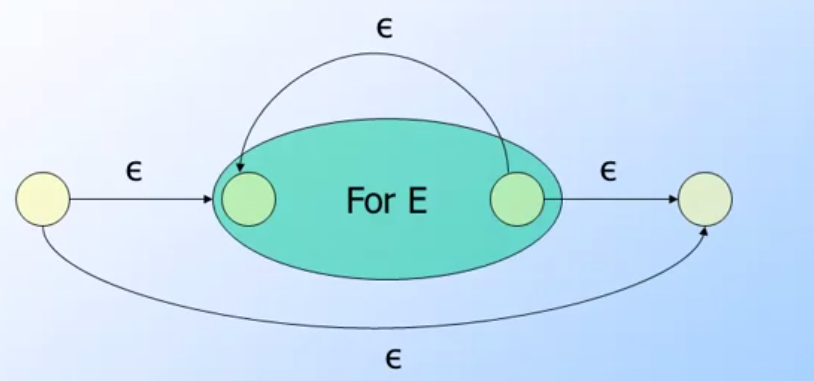
(image from coursera Automata Course)

將RE用DFA表示

概念上就是依照以下的方式:

    狀態(state)也就是我們節點
    而邊線(arc)就是我們會出現的symbol
    所以DFA所能接受的路線(path)就是我們要的語言(language)．

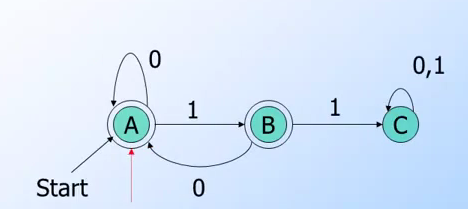
拿前一章節出現過的圖，舉例來說:

• 這個DFA要表達的A->B 的Language可以是{11} 或是 {0011} 或是 {0001} 也可以說L(E)={1,01,0101...}
• 所以這個RE可以表達為E=(0)*1+(10)*1 也就是說
  • 0可以出現一次或是無限次，但是最後一定要有一個1
  • 或是(01)可以出現一次或是無限次，但是最後一定要接著1

k-Path

這邊指的K-Path指的是要透過狀態i到達狀態j其中只能經過k(其中k代表1…k, 比如說k=2 也就是 0, 1, 2)能到達目的狀態的路線，先用簡單的DFA來舉例，舉例而言． 請注意所謂的 k-path不代表必須經過k，是可以不經過的．

由狀態A->B的k-path

• 0-path 也就是A->B不經過任何其他狀態，結果1
• A-path 也就是A->B可以經過狀態A，結果0*1+1，也就是可以走無限個0然後走到B或是直接走到B．
• B-path 可以經過B，也可以經過A(這裏假設 A = B - 1)，當然可以都不經過．所以推導出來也就是整個DFA的RE：也就是 0*1+(10)*1

關於 k-path的推導題

k-path通常指的是由狀態i 到狀態j 必須經過k狀態（其中k代表的是 0, 1, 2, … k)．

    記作 R_ij^(k) (其中 ij 為下標，k為上標)

所以R_ij^(k) 也可以換成思考為:

• 路徑由 i到j 不經過 k (k-path是可以不經過k，也代表經過k個數是0)
• 或是:
  • 路徑由i到k
  • 路徑k走到過所有k-1的狀態回到k
  • 路徑由k走到j

如以下圖:

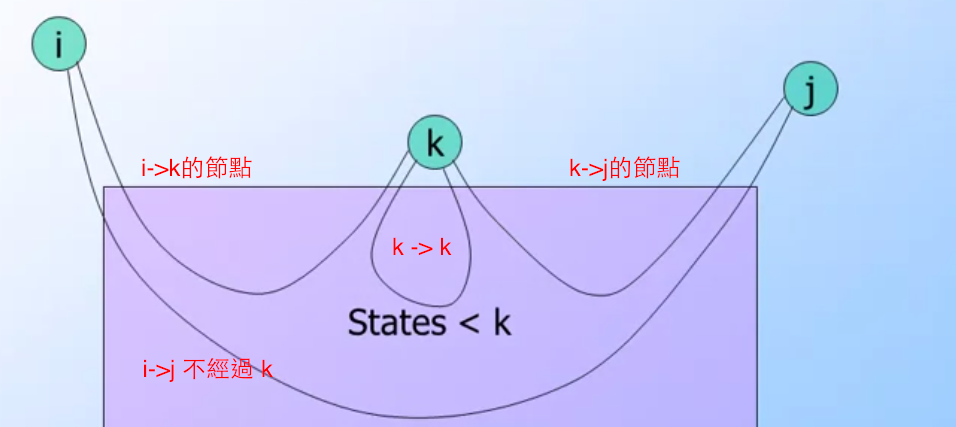
透過以上的圖示，可以推導出公式如下：

    R_ij^k = R_ij^(k-1) #也就是 i->j 不經過 k
            +  R_ik^(k-1)   R_kk^(k-1)*  R_kj^(k-1)   # 就是 i->k, k-k, k->j   

UNIX (REGEX) Regular Expression

接下來，課程談到介紹UNIX上面常使用的Regular Express．這邊大家應該比較熟悉，只把幾個常用符號整理一下:

• [a-c] 指的是 a, b, c 都可以
• [a-z] 同理可證，就是所有小寫字母．
• “+” 指的是出現至少一次．
• “*” 指的是零次或是以上．
• “?” 指的是零或是一次．

還有一些跟RE與NFA跟DFA的轉換可以筆記一下:

• UNIX RE 先轉換成 ε-NFA (並且擁有自己的final state)
• 設定一個新的start state 並且將原本的ε-NFA 作為 ε-translations
• 透過ε-translations就可以轉換成DFA
• 透過DFA可以再度的轉換到RE去

詳細的轉換方式，可以參考以下圖片

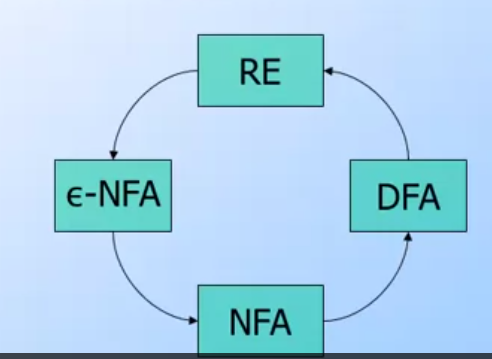
Decision Properties of Regular Language

####定義:

Decision Properties of Regular Language指的是是一個演算法來作為正式敘述一個語言的方式．

舉例:

• Is string w in language L?
• Are those two language the same?

####The Emptiness Problem

指的是給予的Language是不是符合這個RE也就是說，假設是DFA給予的語言，能不能夠從start state 跑到 final state．

####The Infinitness Problem

指的是RE中是否有發生迴圈的圖形． 而檢查圖形是否為 Inifitness 最簡單的方法是:

    如果全部的狀態個數為n， 只要可以接受輸入language個數，而且 m >n．  代表就會有迴圈發生．

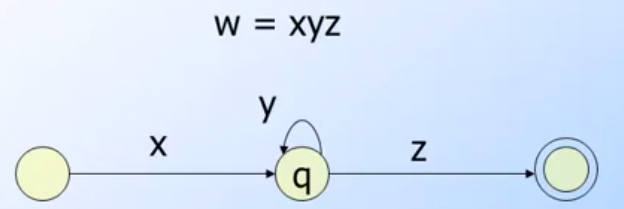
就會像是以上的圖形一樣．

Pumping Lemma

需要先定義一下，什麼是Pumping Lemma，根據wiki上面解釋如下:

    RE中一個長字串，其中有一段文字有出現超過一次以上．

簡單的說，Pumping Lemma 也就是上面圖形所呈現的狀態．

那接下來就要顯示．基礎定義：

• 全部的狀態個數為n，輸入的語言為w
• w = xyz

• xz] <= n

  • 這邊解釋一下

    xz

    代表的是出現的alphabet個數，比如說 x=abca z=bcdb |xz|=abcd

• y

  > 0

• For all i>=0 xy^i z is in L

這幾個定義裡面，最重要的其實是|xz] <= n．因為找出y的方式不是在找出重複的，而是要確認|xz]．以下舉一個例子:

Pumping Lemma 範例:

ex: 語言L他的狀態為1,2,3 輸入為{a, b, c} 輸入為 {abacca}，他們的狀態變化是 1(a)->2(b)->3(a)->2(c)->1(c)->3(a)->2 找出他的w =xyz的pumping lemma

解法：

• 首先試著去找出第一個重複的狀態．也就是1->2->3->2->…
• 這時候抽出2->3的輸入{ba} 即為 y

• 同理，可以分解出前面的x={a} z={cca}．同時驗證

  xz

  = {ac} <= 3

如何驗證兩個DFA L與M 是否equivalence

要證明兩個DFA是否equivalence，需要透過以下方式:

• 計算 L product M
• 找出 w 滿足L也滿足M(滿足:accept 代表能由start state到final state)
• 這樣就可以證明 L與M是 equivalence

接下來，要如何做 L product M方法如下:

• 假設Q1 是 L的所有狀態， Q2是M的所有狀態
• 找出Q1與Q2的start state [q1, q2]
• 開始iterate 每一個transition function，並且找出product DFA
• 透過最後的Product DFA找出一個w 可以由start state走到final state．
• 即代表兩個DFA L與M是equivalence

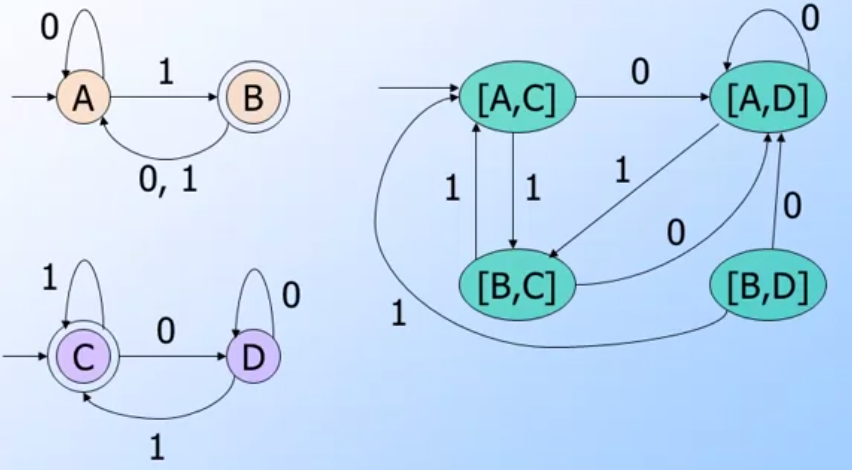(image from coursera Automata Course)

範例:

• 起始點為[A, C]
• 走第一個transition input 0
  • [A, D]
• 走第二個transuion input 1
  • [B, C]
• 依照這個方式… 慢慢建構出所有的DFA如上圖右

Closure Properties of Regular Language

這裏主要是敘述定理，還有一些證明方式，主要定義如下:

• L 跟 M 都是 Regular Language (可以使用regular expression表示出來)

進行以下的操作，並且證明結果都是屬於regular language:

• Union: L U M 仍然是regular language (可以用regular expression來表示)
  • R是L的regular expression， S 是 M的regular expression．L U M = R + S．可以得知 `R + S仍然是regular expression (根據 union law)
• Concatenation / Kleene Star: 根據以上的方式， RS (concatenation)，及 R* , S* 仍然都符合regular expression (concatenation and kleene star law)
• Intersection: L intersect M 代表裡面的 R S要找出交集的部分，使用的方式是將兩個圖形做 product 然後找出product的regular expression 即為 L intersect M．
• Difference: L - M 也會是符合regular language． 根據上一則的方式，透過 product DFA LM 可以找出一個流程是 L 可以由start state跑到 final state但是 M不行． 由於該流程regular expression 是存在於L的其中一個，所以該流程也是符合regular expression． 所以 L - M 也符合regular langugage
• Completement: completement in L = sigma(Σ)* - L sigma(Σ) 是regular languge 當然Σ* 也是regular languge根據剛剛的difference 定理 L - M 也符合regular langugage自然而然 Σ* - L 也是．
• Reversal: L^R 表示Reversal 代表的是 L = {0, 01, 11} L^R = { 0^R, (01)^R, (11)^R}= { 0, 10, 00}
  • 需要注意的是 (0)^R = 0 同理可證 (1)^R = 1
  • 相關的Reversal Law:
    • (F+G)^R= F^R + G^R
    • (FG)^R = G^R F^R
    • ((F)*)^R = ((F)^R)*
  • 範例: E = 01* + 10* + 1 找出 E^R
    • E^R = (01*)^R + (10*)^R + 1^R
    • ` (1)^R 0^R + (0)^R 1^R + 1`
    • ` (1^R)* 0 + (0^R)* 1 + 1`
    • 1*0 + 0*1 + 1
• Homomorphism: h(L)就是透過某些轉換是來把原先的alphabet做一個替換．
  • ex L = {0, 10, 11} h(0)->A, h(1)->B 則 h(L) = { A, BA, BB}
• Inverse Homomorphism: h^-1(L)是將把透過 h(L2)的結果轉換回 L2. h(L) = L1, h^-1(L1)= L

相關程式

我也把NFA的概念加以實現成一個小工具．放在https://github.com/kkdai/nfa

原本根據定義是無法實現，但是我透過BFS還是可以做出來．只是還在思考是不是有遺漏的案例．

參考網址

• Coursera: Automata Course
• Regular_language: wiki
• Pumping_lemma_for_regular_languages wiki